DOI:10.1016/j.ceramint.2020.06.128

利用柔性纳米发电机从周围环境的机械能中获取能量是产生绿色和可再生能源最有效的方法之一。将锆钛酸铅（PZT）颗粒嵌入聚偏氟乙烯（PVDF）聚合物基体中，通过静电纺丝法制备具有0-3和1-3混合连通性的纳米复合纤维。在两个不同的类别下，提出了Maxwell-Garnett、Rayleigh和Tinga等各种理论模型，以预测PVDF-PZT纳米复合纤维的介电常数，并将预测结果与实验结果进行比较。另外，通过Furukawa模型预测压电系数（d33）和压电电压系数（g33）等压电性能，并将预测值与实验值进行比较。最后，导出实验模型来预测具有0-3和1-3混合连通性的二元复合材料的介电常数。与已有的模型相比，该实验模型可以准确预测PVDF-PZT纳米复合纤维的介电常数。对于PZT体积分数1.1和17，理论和实验结果的最高和最低差值分别为12.24％和0.12％。同时，由于介电常数和压电系数之间的线性关系，该模型可用于预测压电系数。

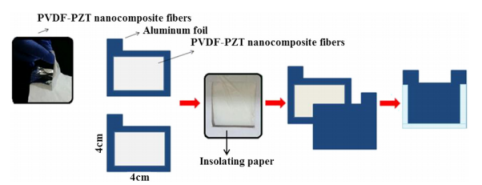
图1.基于PVDF-PZT纳米复合纤维的发电模块的制备示意图。

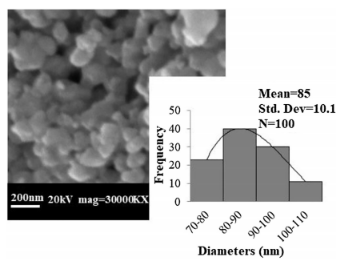
图2.PZT颗粒的SEM图像。

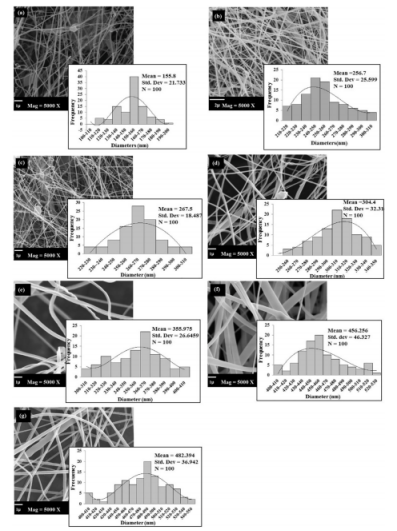
图3.PVDF-PZT纳米复合纤维的SEM图像和直径分布图：（a）原始PVDF纤维，（b）具有0.011 PZT体积分数、（c）具有0.041 PZT体积分数、（d）具有0.096 PZT体积分数、（e）具有0.17 PZT体积分数、（f）具有0.3 PZT体积分数和（g）具有0.37 PZT体积分数的纳米复合纤维。

图4.具有0-3和1-3连通性的PVDF-PZT纳米复合纤维的TEM图像。

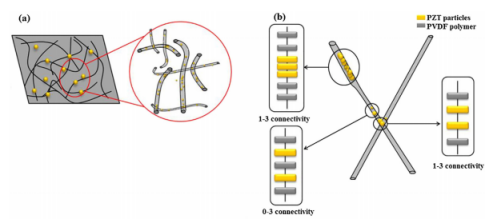
图5.a）具有0-3和1-3连通性的PVDF-PZT纳米复合纤维的示意图，b）在具有0-3和1-3连通性的串联模型中，粒子在其聚合物基质中的分散情况。

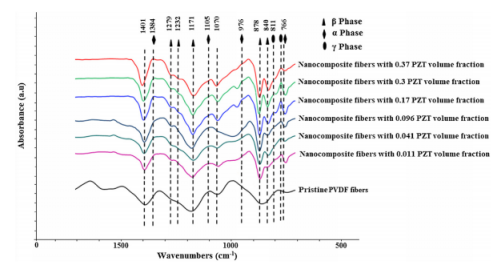
图6.具有不同PDF体积分数的PVDF-PZT纳米复合纤维的FTIR光谱。

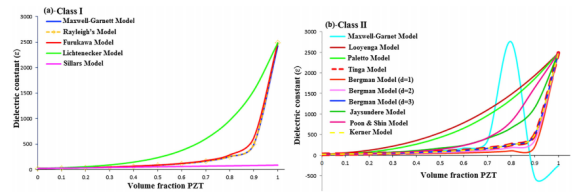
图7.PVDF-PZT纳米复合纤维中I和II类的预测理论介电常数与不同体积PZT的关系。

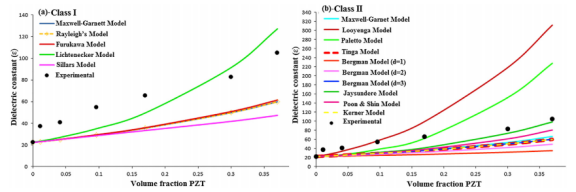
图8.I＆II类理论模型结果与实验结果之间的介电常数比较。

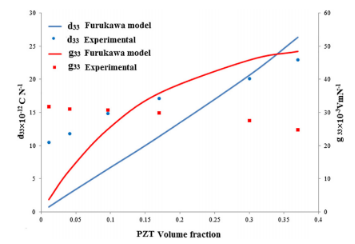
图9.Furukawa模型的理论结果与实验结果的压电系数（d33）和压电电压系数（g33）的比较。

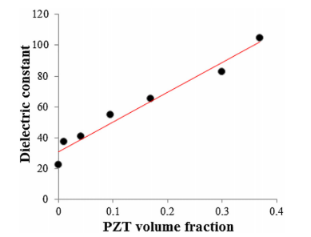
图10.介电常数和PZT体积分数之间的关系。

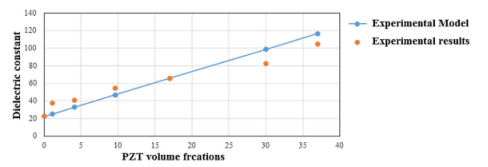
图11.实验模型结果和实验结果之间的介电常数比较。

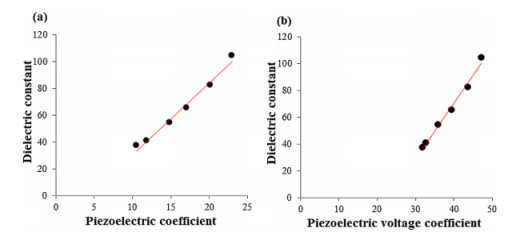
图12.a）介电常数和压电系数之间的关系，b）介电常数和压电电压系数之间的关系。

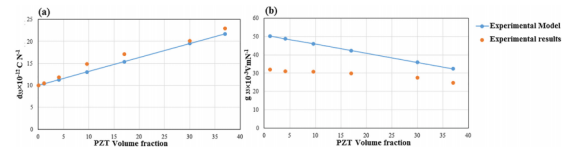
图13.实验模型结果与实验结果之间压电系数的比较。